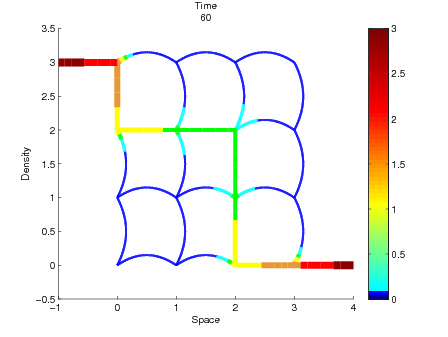
We present some simulations based on the Greenberg-Alt hyperbolic-parabolic (PDE) model of
chemotaxis on networks, which are represented as graphs composed by oriented arcs connected
at nodes. The PDE system is endowed with suitable initial conditions, boundary conditions
at outer nodes of the network and with transmission conditions ensuring the conservation of fluxes
at junctions. The simulation algorithm is based on the Asymptotically High Order numerical scheme
for the hyperbolic part and with the Crank-Nicolson scheme for the parabolic part.
The simulation tool was tested on different networks with two or more source-sink nodes (representing
food sources), and results obtained show that individuals are able to find the shortest path connecting
food sources as happens in laboratory experiments conducted on Physarum polycephalum moving in
a maze, see the paper by Nakagaki et al. on Nature volume 407, page 470 (2000).
In particular, in the example reported below, the network has a source (node 0) and a sink (node 17).
Arcs depicted with straight line have length 0.5, while arcs depicted with curve line have length 10,
then the shortest path is composed by arcs: 1-5-9-10-14-21-25-26.
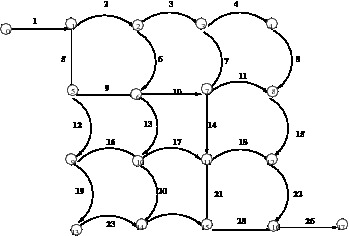
chemotaxis on networks, which are represented as graphs composed by oriented arcs connected
at nodes. The PDE system is endowed with suitable initial conditions, boundary conditions
at outer nodes of the network and with transmission conditions ensuring the conservation of fluxes
at junctions. The simulation algorithm is based on the Asymptotically High Order numerical scheme
for the hyperbolic part and with the Crank-Nicolson scheme for the parabolic part.
The simulation tool was tested on different networks with two or more source-sink nodes (representing
food sources), and results obtained show that individuals are able to find the shortest path connecting
food sources as happens in laboratory experiments conducted on Physarum polycephalum moving in
a maze, see the paper by Nakagaki et al. on Nature volume 407, page 470 (2000).
In particular, in the example reported below, the network has a source (node 0) and a sink (node 17).
Arcs depicted with straight line have length 0.5, while arcs depicted with curve line have length 10,
then the shortest path is composed by arcs: 1-5-9-10-14-21-25-26.