Questo focus è la continuazione di un precedente focus. La flessibilità di una proteina può essere verificata ad esempio dalla misura degli RDC. Il valore di un RDC dipende dall'orientazione spaziale di certi dipoli (spesso le coppie N-H dei vari aminoacidi) rispetto ad un sistema centrato nel metallo. Se il dipolo appartiene alla stessa struttura rigida del metallo, i movimenti saranno solidali ed il range di valori ottenuti (per differenti dipoli) sarà elevato, in quanto le orientazioni possono essere pensate come una distribuzione casuale. Viceversa se il dipolo appartiene ad una struttura che si può muovere rispetto al metallo, i valori misurati saranno le medie sulle varie posizioni assunte. Il processo di media riduce lo spread dei valori, per cui la libertà conformazionale può essere dimostrata attraverso i valori numerici delle misure.

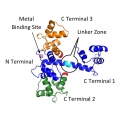
Prendiamo la calmodulina, mostrata in figura. Il normale fold della proteina cristallizzata è mostrato in blu. Quando la proteina è in soluzione la lunga alfa elica che connette le due parti (dette N e C terminale) tende a spezzarsi. Di conseguenza il C terminale, ancora connesso da una parte flessibile non mostrata, può assumere differenti posizioni, due delle quali sono mostrate in figura con i numeri 2 e 3.

La scala temporale delle singole fluttuazioni è di diversi ordini di grandezza più corta del tempo necessario ad ottenere gli spettri NMR, per cui le informazioni sulla flessibilità si potranno ottenere solo come funzione di probabilità sull'insieme delle posizioni consentite.

Il problema è severamente sottodeterminato. Al massimo 25 vincoli possono essere ottenuti da un qualsiasi numero di RDC (si veda ad esempio questo articolo). Negli ultimi dieci anni differenti metodi sono stati proposti per determinare la migliore soluzione, utilizzando differenti modellizzazioni e misure. I metodi proposti posso essere raggruppati secondo due differenti approcci.

Un primo approccio è cercare la soluzione che minimizza le ipotesi addizionali sui dati, attraverso il Principio di Massima Entropia (MEP). La soluzione MEP massimizza l'incertezza sui dati, per cui ogni caratteristica mostrata da questa soluzione è rilevante. D'altra parte la soluzione MEP è in generale una funzione continua di probabilità, per cui un grande numero di stati è necessario per ottenere una sua approssimazione. Il gran numero di variabili coinvolte pone non semplici problemi computazionali.

Un secondo approccio è quello di determinare se le misure mostrano qualche preferenza per qualche posizione. La Massima Probabilità Ammissibile (MAP) è il massimo peso che può essere dato ad uno stato in una distribuzione di probabilità compatibile con le misure. Come funzione dello stato la MAP non è una distribuzione di probabilità, ma una maggiorazione ottimale dei valori delle distribuzioni di probabilità che ricostruiscono i dati. Le zone dove la MAP è grande sono le zone dove si possono concentrare le asimmetrie delle misure. D'altra parte non è possibile stabilire fino a punto la vera soluzione mostra queste asimmetrie.

I due approcci coincidono nei casi limite, ovvero quando la flessibilità è bassa, ovvero quando non vi sono vincoli agli stati assumibili. Per approfondire il tema, seguite il link proposto.